A review of the paper “ Singularity avoidance in Bianchi I quantum cosmology” – Claus Kiefer, Nick Kwidzinski, Dennis Piontek
A Cosmic Debate
The universe is a very big place. To call it big is an underestimation, the size of this cosmic structure is beyond anyone’s imagination of “big”. In numbers it is estimated to be 93 billion lights years across, meaning it would take you 93 billion years to cross it that is if you were travelling at the speed of light, and that’s almost 9 times the age of the universe !
A study of the universe means a study of its structure, mechanism, and evolution, all of which are still an ongoing debate since thousands of years. Just recently [ as of the publish date of this article ] was there a published Nature paper claiming that the universe is closed in shape, despite the modern consensus that it is flat, based on the ΛCDM (Lambda cold dark matter) or Lambda-CDM model. This new study still requires a lot of inspection, but if it is correct, cosmology is in for a crisis, suggesting a reformulation of the current model and our view of the cosmos. But one thing that everyone agrees on, is that despite how the shape of the universe is, it exhibits points in space that are ill-defined, points that we call singularities, and that is what we will be focusing on in this article. What are these singularities ? and how can we avoid them ?
Einstein, Singularities and COSMOLOGY
Our starting point will always be Einstein’s theory of General Relativity (GR). The theory has proven itself once and again over the past century that it is unshakable, passing tests and predictions that Einstein claimed back in 1915 when he published it. However, GR is incomplete, in the sense that it is not the final theory of gravity, and we know so for several reasons, one of them are the presence of these singularities. Let’s take a step back and explain how GR works and why the presence of singularities pose a problem.
General Relativity is a theory of gravity, explaining how everything in the universe from large scale structures such as the planets and stars to particles such as the photons move through spacetime-this 4 dimensional fabric that Einstein proposed that laid the foundation of his theory. One can visualize this spacetime as a flat sheet of fabric, capable of bending and curving. Massive objects such as planets and stars have the ability to bend this spacetime, causing a curvature. The more the mass of this object, the more the curvature.
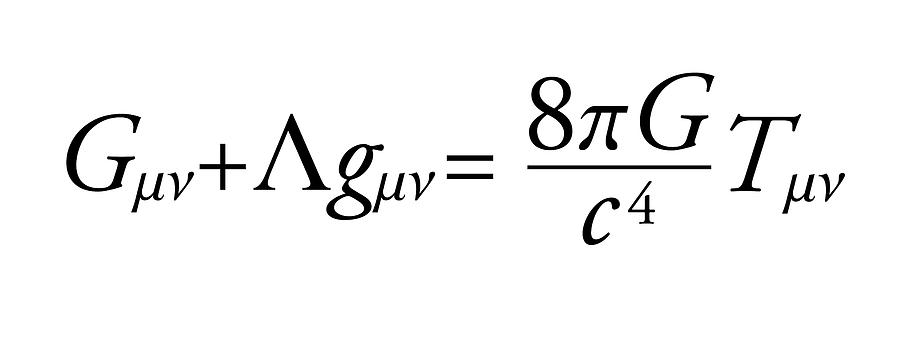
Objects in space then follow a curve caused by the curvature of some other massive object, the same way the moon rotates around the Earth based on the curvature Earth is causing, and the same way the Earth goes around the Sun caused by the Sun’s curvature.
But what happens if an object is so massive beyond the mass of a star ? At some point, spacetime gets punctured, like a hole in a sheet of fabric. We call this hole a singularity, and are caused my extreme massive and dense objects we call Blackholes, and the motion of objects around blackholes is unknown, their trajectories are ill-defined.
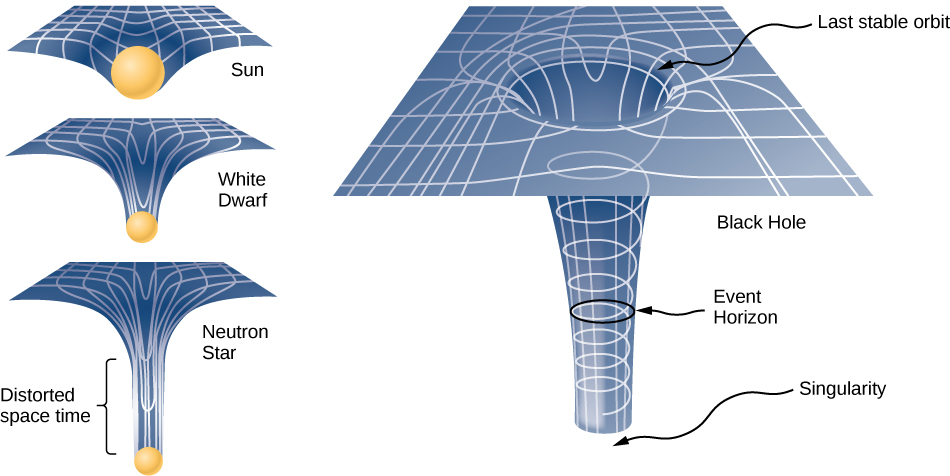
Credit: (modification of work by NASA)
In other words, singularities mean that spacetime doesn’t make sense anymore, and Einstein’s Field Equations fail, in the sense that the equations blow up, showing infinities and undefined values. Infinities in physics are a catastrophe, they are a signal that we did something wrong in our equations which are in urgent need of correction if we hope for any further investigation. This is one of the reasons that I’ve mentioned that tells us why GR is incomplete.
So far we have spoken about singularities caused by a gravitational collapse, that is singularities from blackholes, but one can extend GR to study the universe globally, as a whole. Here one enters the realm of cosmology, and again faces singularities; cosmological singularities.
The current accepted cosmological model today is the lambda-CDM model we mentioned in the beginning. It is the model that explains the universe, its content and its evolution through the Friedmann equations. These equations assume a homogeneous and isotropic universe, which means that the universe looks the same in every direction and despite from where you look at it. This is known as the cosmological principle and it is one of the foundations of the lambda-CDM model. But no matter how much you tweak and twist the Friedmann equations and fix the parameters in it, we’re always going to end up with a singularity somehow. A famous singularity which results from these equations is the Big Bang. The Big Bang – a scenario explaining the beginning of the universe – is a cosmological singularity where physics near it doesn’t make sense anymore, we simply cannot understand how physics works there. Another cosmological singularity is the Big Crunch – a scenario of the fate of the universe – also exhibits the same behavior as the Big Bang, where we encounter ill-defined values and our equations blow up. To understand the beginning and the fate of the universe means we need to get past these singularities, and to get past these singularities demands a different approach to how we see gravity, it demands quantum gravity.
Quantum Gravity, an awaited hero ?
A quantum theory of gravity is not available in final form. There are many approaches to a theory of quantum gravity (QG) from string theory to loop quantum gravity, all of which are attempts to unify quantum theory with a theory of gravity, an attempt which promises a solution to many of the problems faced by GR, one of which is the problem with singularities, and also other problems faced in Quantum Field Theory.
One of these approaches is Quantum Geometrodynamics-which is an extension of Einstein’s theory of gravity to the quantum world, with the Wheeler-DeWitt equation as its central equation shown in Fig.3.
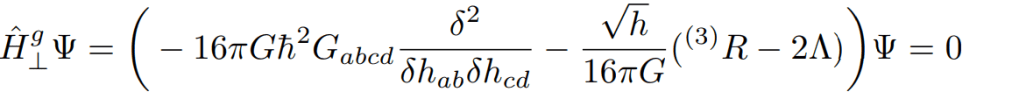
Intimidating as it looks, the Wheeler-DeWitt equation is a field equation whose solution is ψ , the wave function of the universe. [the name “wave function of the universe” dates back to 80’s to a paper by Stephen Hawking and James Hartle who tried to explain a model of a universe without any boundary or beginning. Their model had some inconsistencies and sparked countless arguments. Nevertheless, the solution which they were looking for lies in a more fundamental equation written in 1967 by John Wheeler and Bryce DeWitt, the above mentioned Wheeler-DeWitt equation].
It is still an ongoing debate what exactly this ψ is and how to define it, but physicists hope that it would be able to tell us about the behavior of the universe near singularities, similar to how the wave function ψ in the Schrödinger equation tells us about the behavior of a quantum system of particles. In this equation, the quantum system is the whole universe studied near singularities where it behaved quantum mechanically. However there is a price to pay using this approach. Treating the universe as a quantum system gives rise to fundamental problems, mainly the problem of time, but this is beyond the scope of this article.
DeWitt already discussed the problem of singularity avoidance in his pioneering paper of 1967. He imposed the condition that the wave function of the universe ψ should be 0 for a singularity to be avoided (DeWitt criterion). This is because ψ is a functional – function of a function – of the three dimensional geometries known as the superspace. Each three dimensional spatial geometry is the space defined by the metric tensor h. One can see the superspace as the space of all spaces.
Near a singularity, the three-geometry is said to be singular, loosely speaking there is no more three-geometry, and hence why DeWitt expect the vanishing of ψ which is made up of these three geometries.
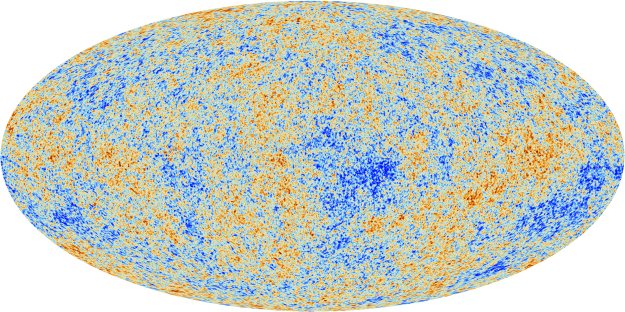
Credit: ESA, Planck Collaboration
In their paper, Kiefer et al. took a step forward and discuss the issue of singularity avoidance for anisotropic cosmologies, that is universes that do not look the same in every direction. The cosmological principle which is the foundation of the ΛCDM model is no longer present here, in fact, it was never a necessity to begin with, just an idealization to make the work easier. Truth is, the universe does indeed look anisotropic when looked at from the Planck satellite through the cosmic microwave background radiation (CMB) shown in Fig.4.
A generalization of the model to account for anisotropic universes means one would expect more criteria where singularities can be avoided. This was shown to be true by the authors who uncovered 3 criteria in order to avoid singularities in anisotropic universes.
Criterion 1: A singularity is said to be avoided if ψ goes to 0.
Criterion 2: A singularity is said to be avoided if the current density or flux of ψ is 0 .
Criterion 3: A wave packet is said to avoid the singularity if it spreads in the vicinity of the singularity.
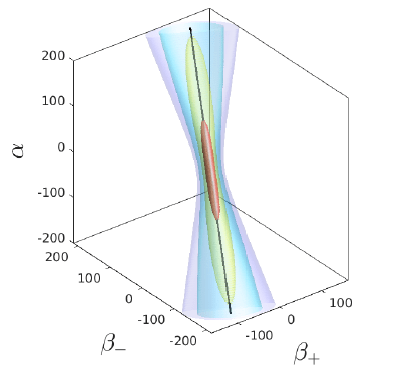
It is still not fully understood how to interpret such criteria, what does it mean to say the flux of the wave function of the universe? And how does a wave packet spread? It is left for future work to make sense of these results.
Kiefer et al. further investigate these criteria for different anisotropic models such as the Kasner model and Bianchi I models to which the name of the paper refers. They have showed that all the criteria pass and thus a singularity is avoided in anisotropic universes.
Conclusion and the Fate of Singularities
Singularities pose a big problem in physics; they are a red light that should be avoided or else our equations blow up and our understanding of nature collapses. The theory of gravity exhibits a lot of them, it is a call for physicists to study gravity beyond what Einstein taught us. A quantum theory of gravity is needed. Wheeler and DeWitt suggested one approach known as Quantum Geometrodynamics. Kiefer et.al used this approach to investigate if it allows us to avoid these singularities. They showed that anisotropic models such as Kasner and Bianchi I models do indeed avoid singularities based on the 3 criteria they have found. However, the authors’ investigations were done on hypothetical models. A more accurate model that describes our own universe would be the Bianchi IX model, but attempts using the Wheeler-DeWitt equation on it will be the subject of future investigation.
Quantum gravity is still a work in progress, and any theoretical or cosmological result should be taken with skepticism. After all, Einstein’s theory of Gravity was at some point a work in progress, and the scientific community took it with a lot of skepticism.
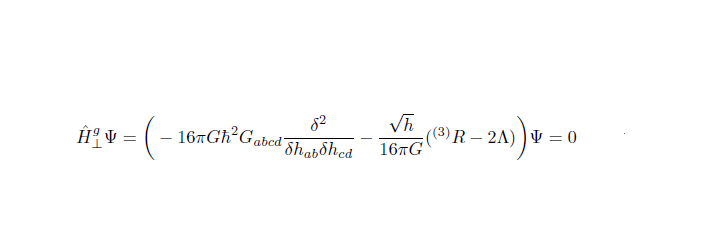
Leave a comment